Automated Market Makers (AMMs) have changed the way of exchanging tokens in the world of DeFi. DEXs such as Uniswap, Pancakes, and Balancers all employ AMMs. Liquidity providers (LPs) on these DEXs can earn fees on swaps of different token pairs. Curve finance was introduced on the same lines in January 2020, and has marked a year in the DeFi space. Its main motive was to offer low slippage exchange of tokens by only having pools of similarly behaving assets such as stablecoins. Curve StableSwap is an automated market maker that enables the users to swap between same flavoured coins with low slippage and fees. LPs can add their tokens in any pool of the curve and gain fees charged on transactions. Unlike Uniswap which focuses more on maximising liquidity. With higher risk of slippage. Moreover the latest version of Curve StableSwap known as Curve Finance allows the user to swap between unpegged assets as well. Like other decentralised exchanges that require ETH for trading for instance in Uniswap you can not trade a stablecoin directly, Uniswap will change your stablecoin into the ETH and then trade ETH for the stablecoin. Which results in two trades causing higher expensive fees. The Curve StableSwap pools allow the user to worry less about the less price impact over the trade. Since all the pools are 1:1 stable pools that are USDT/DAI or 1:1 synthetic stable pools that are sETH/ETH, keeping liquidity pools restricted to similar assets the impermanent loss is not the thing to be concerned about. The StableSwap AMM model is the combination of both Uniswap and Linear Invariant curves. So in order to understand the model we will first understand what is invariant An invariant is a property of a mathematical object which remains unchanged after operations or certain transformation. A linear invariant model is described as x + y = C Where x and y are represented as the pool tokens and C is sum invariant. x+y = C y= C- x The constant sum is the equation of the straight line formula which is graphed below In order to understand the linear variant let's go through some examples. First let's calculate constant if we have 90 tokens of X and 90 tokens of Y then C will be: If Alex wants to sell 23 X tokens how many Y tokens will she receive ? Alex selling tokens X tokens will result in an increase in Y tokens in the pool. Since the constant must remain the same. We have to find Y. The number of Y tokens after trade will be 67 which means we need to find how many she is going to receive after the swapping of X tokens. Alex will receive 23 Y tokens if she sells 23 X tokens. The pools are now 113 X tokens and and 67 Y tokens To calculate the price will do Where delta y is how much was withdrawn and delta x is how much was deposited The rate was exactly 1. 1 X token for 1 Y token. The price we calculated above can be stated as the gradient or the limit of the small trade there the derivative of the price is If the tangent in the graph is steep we can say that we get more Y for less X i.e Y is cheaper OR If the tangent is shallow one can get less Y for more X i.e Y is expensive. Therefore taking the derivative to graph tangent: So from the derivation we can see that when the pool is balanced the price is equal to 1 With the linear invariant constant sum formula we are likely to have zero chances of slippage which is also known as infinite leverage. Though, linear invariant helps to keep the price constant but it can also drain the pool entirely. The Uniswap AMM works on constant product formula x*y=k Where x and y are the pooled tokens and k is the variant of their product. Solving for y to get the equation of the curve: x*y=k y=k/x Below is the representation of the Uniswap AMM formula curve. The Uniswap AMM model always makes sure that there is always liquidity in the pool. In order to understand the model of Uniswap let’s go through the following example. If there are 95 token of X and 95 token of Y then k will be If Alice wants to buy 19 tokens, how many X tokens should she deposit in the pool ? Since 9025 is constant variant, then removing 19 token of Y from the liquidity pool will result in 71 Y tokens This means that X tokens will need to be increased from 95 to 119 to preserve the constant k. Now we will take the difference of X for before and after the swap Therefore Alex needs to deposit 24 X tokens in order to receive 19 Y tokens. Calculating the price per token we get Therefore 1Y token costs 0.79X token If Alex does the another transaction of 24X for Y: Then we calculate the constant product invariant: The value of Y is 63.1118881119 now we calculate the difference after and before the swap So Alex will gain 12.8881118881 of Y tokens when 24 tokens for X are being traded. Hence the price for this trade will be: There price for 1Y token is 0.537004662 X tokens After the trades there was an increase in the value of X tokens and decrease in Y tokens which resulted in a decrease in the supply of Y tokens and hence Y became more expensive for k to remain the same. The price in Uniswap is adjusted after every trade. delta y/ delta x =slope Taking derivative: The graph of the curve is represented below and the slope is represented in red line: If users continue to buy Y tokens this would mean there will be more X tokens in the pool declining the supply of Y in the pool. According to the order book the more we buy the Y token the more we move up the curve. The price and volume are set by traders. In Uniswap AMM the constant product variant xy = k and the depth of the curve indicates the slippage. Where depth indicates the liquidity of the pool. Now let's study the model of Stableswap. Up till now we have studied that the linear invariant has no slippage but that is not an ideal scenario because such pools can run out of tokens any time. On the other hand the constant product invariant that is self regulating makes it expensive in order to bring the pool back to the balance. Therefore stableswap combines both the methods in order to find the middle way where pools would not run out of the assets nor do the traders have to face expensive trading. In stableswap the pool can slide up and down along the curve x+y=k when it is balanced and the price is at $1. When the pool becomes unbalanced it converts into product invariant resulting in expensive trades. The stableswap has kept different stablecoin in its pool in order to keep the pools balanced. And the formula looks more like x+y+z=k and x*y*z=k The stableswap AMM model is stated as The AMM is the sum of both linear invariant and product invariant. For example, For a USDC+DAI pool: And Adding them becomes Generalized as Where n indicates the numbers of tokens n= 0,1,2,3.. Generalising the equation in terms of y Taking derivative of the above equation we get Therefore the graph of the above equation is represented as below: The representation resembles the x*y=k curve because we have not amplified the linear variant. The reason behind the amplification is that it helps to magnify the linear invariant part of the formula to allow for low slippage. As we increase the amplifier the bonding curve will look more like the linear variant. Therefore the mathematical representation becomes after multiplying chi on both sides. Which helps to focus more on the low slippage part of the equation. This is often called an amplified bonding curve. Taking derivative of the equation: Graph of the equation when chi is 0.53 Ideally in Stableswap, the curve is linear so can be called as the function of X and Y We multiply the sum invariant by D so that chi will not depend on the number of tokens in the pool. The sum invariant formula becomes (where n donates the dimension) The stableswap formula will become: In order to make the formula adaptive to in every situation, we add a fixed constant A in the formula of chi: The value of in a balanced pool when X is 25 and Y is 25 And when the pool in unbalanced X is 3 and Y is 50 Therefore when the pool starts to become unbalanced the curve starts to look like product invariant or Uniswap curve. Whereas A is the constant number chosen the protocol and named as amplification coefficient Now the stableswap invariant becomes Hence the stableswap generalised model is: Stableswap has entered the market as a competitor to Uniswap and other DEXs, providing its users a chance of low fee trading and also allowed them to trade directly between the stablecoins. Its AMM has been designed neatly which ensures the low or no slippage and keeps liquidity balanced in the pool. However if we look around the AMM models more keenly designed only for the liquidity resulting from expensive trades and high slip risk in the market. You can also read upon our latest publication on Gas Tokens.Introduction
What Makes StableSwap Different
Understanding The Maths Of Linear Invariant Sum And Product model
Linear Invariant
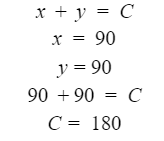
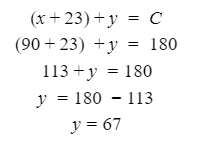
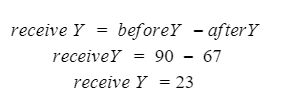
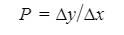
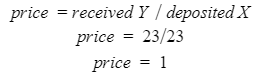
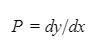
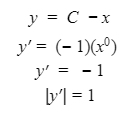
Uniswap AMM
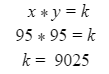
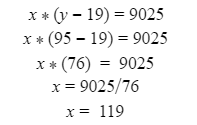
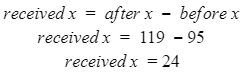
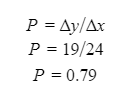
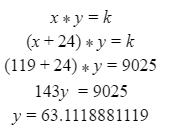
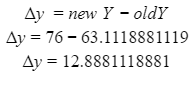
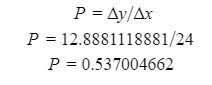
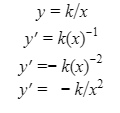
Source: https://miguelmota.com/blog/understanding-stableswap-curve/StableSwap AMM:
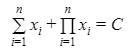
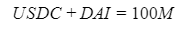
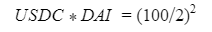
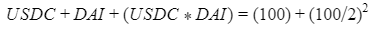
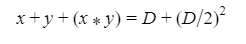
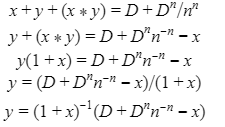
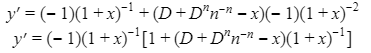
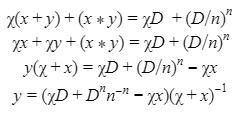
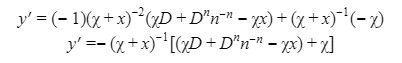
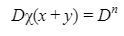
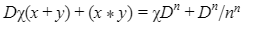
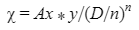
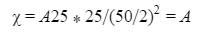
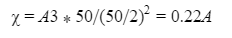
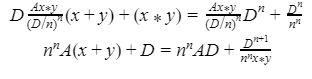
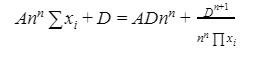
Conclusion:
References:


