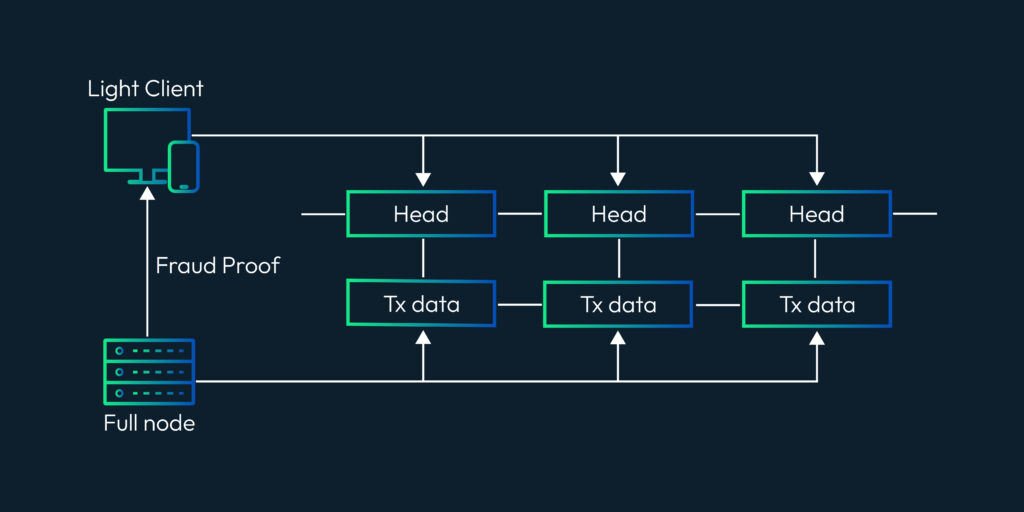
In recent times, we on twitter are witnessing a frequent discussion about the Data Availability Problem and its importance. There is no doubt in how L2 solutions are empowering ethereum's vision to be a global super computer. However, we can't deny the fact that even with L2s we can't achieve what we have envisioned due to number of limitations. Out of them the first and the most important one is "The Data Availability Problem(DA)". So in this series of we are going to take a deeper look in what DA is and how can we solve its challenges with Data sampling and Fraud proofs. Let's briefly discuss what this series is about? And what are the topics that we are gonna cover to fully understand the concept of DA Proofs. In this particular post we are gonna talk about what is Data Availability, why it matters to us and what are the potential schemes to solve this problem. We will also discuss how a node can submit a fraud proof in case of detecting a malicious transaction at L2. We already know that the cryptocurrency platforms are gaining traction on daily bases. This massive adoption comes with the scalability limitations for existing blockchains. One possible solution for this problem is to simply increase the on-chain throughput by improving the hardware specifications. However, if we tend to do this, this would hurt the decentralization as very few nodes will be able to participate due to large hardware requirements. As a result most of the nodes will run the light clients and rely on the full nodes to verify the blockchain state. This reliance guarantees weak assurance in a case where the majority of nodes are dishonest. This is the main reason why L1s are considering off-chain solutions as the best alternative to achieve scalability. When we talk about off-chain solutions such as Rollups, we often tend to ignore the fact that even with rollups we can’t achieve unlimited throughput. Ever wondered Why? This is because the rollups are an off-chain computing solution which performs the state calculation off-chain. However, in order to finalize the block they do need to publish the state and callData to the base layer such as Ethereum. So even if we make the sequencer, a supercomputer to produce infinite blocks we can’t finalize them because of the network and storage limitations at the base layer. So now when we have acknowledged that rollup itself can not achieve an unlimited throughput, we have another problem which is what if the centralized sequencer itself is dishonest? And he has computed a false state? How can L1 reject those transactions? Well in that case we have full nodes on the base layer. These nodes are watching the state and on detecting a faulty transaction they can submit the fraud proof to mark the block invalid. Does that mean all the L1 nodes responsible for watching the rollup activity, need to download the whole sequencer data?? Well, yes that is exactly the case. This implies that even by proposing off-chain solutions we are still demanding full nodes to increase their hardware requirements. That's bizarre right? On top of this, if somehow you manage to run a powerful node to watch over the transactions, this still doesn’t guarantee that the sequencer is not trying to cheat by withholding the data. Because even if 1% of data is unavailable then no node can reconstruct the state and hence nobody can submit the fraud proofs within the defined time making the block valid. This is what we define as the “Data Availability Problem”. Heww!!! That's a lot to grasp right?But bear with me. We have some very fun things to discover. And to be honest there is no need to panic as Ethereum has proposed another smart solution to tackle this problem which is “Data Availability Sampling”. So what is Data Availability Sampling? well it allows us to ensure data availability without requiring nodes to download the entire data. This is a massive breakthrough to achieve scalability. So we have two notions: 1- The sequencer is trying to cheat with a faulty transaction but does not hold any data. 2- The sequencer is trying to cheat with faulty transaction and has also withhold some percentage of data so that nodes may not able to reconstruct the block for providing fraud proofs. To explain our purpose of writing we want to prove that the light nodes will not accept blocks with invalid transactions under the influence of dishonest majority in consensus nodes. As an example for the first notion, we are assuming a scenario where a malicious sequencer is trying to cheat by including a faulty transaction in a block but without holding any data. In case of optimistic rollups, to prove that some block is invalid the nodes need to reconstruct a block and submit a fraud proof for it. Now lets discuss a few things which are must for a sequencer to publish on L1 in order to verify l2 state. The block structure is very important when it comes to support the generation and validity of fraud proofs. To describe this we have a block header hi at height i contains the following information. In an account based model such as Ethereum the key value pair are account address and balance. The state needs to keep track of all the data, for example the total fees paid to the block producer. Now to begin with, we define a transition function which performs transition without requiring the whole state tree, but only with state root and Merkle proofs of parts of the state tree that the transaction reads or writes, which is most commonly called “State Witness”. These merkle proofs are effectively expressed as a subtree of the same state tree with a common root. The function could be defined as: t→ Rollup Transactions w→ Merkle proof of transaction tree The witness w consists of a set of value - pairs and their associated Merkle proofs in the state tree. After executing all the transactions t on parts of the state given by w if the transactions modifies any state then, the new resulting NewstateRoot can be generated by computing the new root of the new sub-tree with the modified leafs. If w is not the correct witness and does not contain all the part of the leaves required by the transactions during the execution then it will throw an exception error err. For the rest of this series we will have a few notations which i am concluding here: The innerRoot is the representation of intermediate roots within a block after applying a certain number of transactions. When we talk about rollup state validation, data is the most important thing. Data helps us to reconstruct the state and verify either the state published by the rollup is valid or not. That's why its very important to communicate the DataRoot to the light clients. So lets first understand why and how we can construct the DataRoot. dataRoot i is a fixed size of transaction data chunk in bytes known as “shares”. The share will not contain all the transactions rather a fixed part of transactions. We reserve the first byte in each share to be the starting position of the first transaction. This allows the protocol message parser to establish the message boundaries without requiring every transaction in the block. Given a list of shares (sh0, sh1, . . . shn) we define a function parseShares which parses these shares and output a list of messages (m0, m1, . . .mt) which are either transactions or intermediate state roots. For example, parseShares on some shares in the middle of some block i may return (trace1i, t4i , t5i , t6i ,trace2i). We can not include state roots after every transaction so we can define a period, for example after p transactions of g gas we can include an intermediate state root within a block.Thus we have a function parsePeriod which parses a list of messages and returns a pre-state intermediate roots tracexi and post-state intermediate root tracex+1i and a list of transaction (tig, tig+1, . . .tig+h) such that when we apply these transactions on tracexi , it must give us tracex+1i . If the transactions do not follow the condition then the function must return an err. What if a malicious sequencer has provided us with an incorrect stateRoot? We can check the invalidity of the stateRoot by a function “VerifyTransitionFraudProof”. This function takes the fraud proof submitted by full nodes and verifies it. A fraud proof consists of the following things: The VerifyTransitionFraudProof function applies the transactions of a particular challenged period to the pre-state intermediate which must result in intermediate post-state root. The function VerifyTransitionFraudProof returns true if all the given conditions are true otherwise, false will be returned. Now that we are aware of both DA and fraud Proofs we are now moving with a second notion as we have discussed which is what if the sequencer has computed an invalid transaction and I as a light client detects it. Now I need to compute a fraud proof for it. However, the sequencer has not published the entire data through which I can reconstruct the state to verify. For this problem Rollups like Optimism has proposed a solution which is to enforce the sequencer to publish the data. But how exactly? I am leaving this for another post. Till then adiós. This article has been inspired by the research publication of Mustufa Al-Bassam on Fraud and Data Availability Proofs. To read on rollups and its types refer to this article.The Rollup Block Structure
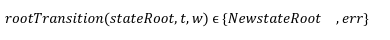
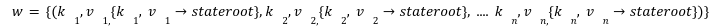
Notations:

What is the innerRoot?
What is DataRoot?

How to Verify the Invalid State Transition?
What is a Fraud Proof?