For the last few years, quantum computers have been in the news and mathematicians and cryptographers are concerned with dealing with the post-quantum attack on the blockchain. Luckily they have come up with the solution that is known as lattice-based cryptography. So you might be wondering what is lattice-based cryptography and what is its potential to deal with quantum computers. In order to understand lattice-based cryptography lets first discuss about lattices and its property. A lattice is a set of points in a vector space with a periodic structure. Which can be described as linearly independent vectors B = (b1,....,bn), i.e, L= L(B) := {i=1kxibi|xiZ}=BZk Where k = the number of column of rank of lattices Since we know that lattice is a subgroup of real numbers in n dimension, we can consider the quotient group as Rn/L of cosets where coset c can be represented as c+L= {c+x | x L} Successive Minima: Let L Rn be a lattice of rank k. For i [k] the i-th successive minimum of L is defined as Determinant of a Lattice:. Let L = L(B) . the determinant, or volume of lattice is defined as The notion of volume is useful to estimate the first minimum of a lattice. The notion of volume is useful to estimate the first minimum of a lattice. The Gaussian set of rules surmises that the number of lattice points in a convex body S (we will usually consider a ball) is equal to the volume of S divided by the volume of the lattice. Using the heuristic with a sphere of radius lambda1 (L) gives the following approximation Let's define a dual of the lattice. A Dual of a lattice can be defined as following Before we start with the lattice cryptography let's go through the concept of the Gram Schmidt Orthogonalization is an algorithm that takes as input a basis B of a vector space and outputs an orthogonal basis. The GSO is valuable in both cryptography and cryptanalysis. Moreover, let us study one more important concept before moving towards the gaussian property of lattice. In most lattice-based cryptography, we consider lattie in a specific form that is obtained through SIS problems. An SIS problem is where we introduce a challenger sample and an adversary where the adversary helps to find the solution of SIS. Then such solutions provide the lattices in Q-ary form. Lattice has one important property that is known as discrete and continuous Gaussian. This thing is important as it helps to form a rejection algorithm that is used in zero-knowledge which helps us to prevent leaking important information. Gaussian function can be defined as : For any integer n is greater than and equal to 1 and sigma is greater than 0 the n-dimensional function spherical Gaussian function. We define discrete Gaussian function over the coset c+L of L belongs to Rn with standard deviation and following probability density function. Let’s define the computational problem of lattices which helps us in the security analysis of cryptography. Suppose that we are provided with a long basis for some lattice L. Then the shortest vector problem demands us to find a grid point in L as close as possible but not exactly equal to the origin point. This might seem a very easy problem but in reality, they are difficult ones to determine due to which they are categorized as NP-hard problems. It is hard to find the short vector as we are given a relatively very long basis. Moreover, when it comes to lattice-based cryptography we are talking in a very higher dimension such as 10,000 and more. Suppose that we are provided with a very long basis of some lattice L. Moreover, we were given a randomly chosen challenge point P. The closest vector problem asks us to find the closest lattice point on L to the challenge P. It is the same as an approximation of shortest vector problem but with a promise, it, can be defined as given an n-dimensional lattice L, gamma(n) greater than equal to 1 and a target point t belongs Rn with the guarantee that dist(L,t) < d = lambda 1(L)/2(n). The unique shortest vector problem was designed considering the worst case of lattice problem. In gamma-uSVP we are required to find the shortest vector in a lattice that is times smaller to the next non-parallel vector in the lattice. Majorly most of the lattice-based cryptography models are built assuming the worst hardness case of Short Integer Solution and Learning With Error. Their efficiencies can be improvised using Ring-SIS and Ring-LWE problems. The Module-SIS and M-LWE is the bridge that connects the both ends. 2. Module Learning With Error: Unfortunately the both of the above problem collapse when SIS and LWE when d =1 and to R-SIS and R-LWE when n = 1 3. NTRU In this section, we will introduce the methods on which we will be judging the level of hardness of M-LWE and M-SIS. The first will be Lattice reduction algorithms: The aim of this algorithm is to find the short basis of the lattice. This technique can be fulfilled using the BKZ- beta algorithm where the algorithm finds the shortest basis of lattice in the - dimension. However, when the algorithm is run over the lattice L in dimension n the first basis output will be: On the other hand an invariant of the BKZ beta- algorithm guarantees that the vector bn-beta-1 will be such that ||b`n-beta-1|| is norm of the vector obtained from the lattice L that is orthogonal to b1,.....bn-beta-1 . Let us assume L contains a very short vector v and it is taken uniformly on the radius of the sphere ||v|| then the expected norm of the projection of v against b1,.....bn-beta will be and the geometric series assumption will be which tell us that the following series will break when therefore we can conclude that the BKZ- algorithm can recover full vector v. Another criteria is by solving M-SIS and M-LWE Solving M-SIS and M-LWE. were dm is the dimensional lattice of volume qdn. if B is larger than it shows it will approximate the SVP and we will compute the Hemrite root that is necessary to solve the parameters of M-SIS. Were Hermite factor will be treated as Now we find the block of size and apply BKZ- algorithm to find the shortest vector z. When B is smaller than the vector being approached we use a different method to solve our problem, which means that we have a unique SVP and we need better approaches to solve our issue. Therefore, we use M-LWE to solve this problem. e Dsigma,Rn we have Mz = 0 mod q where M= [A | Idm |b] belongs to Zdmxd(m+n)+1 where z is a column matrix consisting elements s e 1 we are thus looking for a vector of norm in the lattice L(M)1/q of volume qm/(n+m) and, hence the Solving SVP: Since we know that BKZ beta- algorithm can find the shortest vector only in dimension it will be crucial to solve the problem, therefore, we use two different approaches to solve the SVP one of which is Enumeration method this method has the complexity for the worst case the algorithm works fine on the blocks of size beta = 40 or 50 However, the super-exponential condition makes them useless. Hence, under such circumstances we use another algorithm named sieving algorithm. In this algorithm the program first proceeds by sampling the exponential number of lattice vectors and then obtaining the increasingly shortest vector obtained by the difference of the shortest vectors that are close to one another. The best sieving algorithm have the heuristic complexity of 20.292 which can be reduced to the complexity of 20.256 by using Grover's quantum search algorithm. A trapped door is a one-way function and it is hard to invert when it is accessed through a secret trapdoor in lattice a trapdoor is written as We can see that the set of element x such that Ax= 0 forms a lattice and provide solutions to fA ( x ) = t that forms a small coset of this lattice. The lattice trapdoor will allow us to sample small vectors in to the lattices the algorithm was introduced by Gentry which is known as GPV trapdoor in which he said in order to form a lattice-based trapdoor one needs to input the shortest basis B of lattice L and outputs a form of Dc+l, for any coset c+L and standard deviation of which depends on the size of basis B. However this is a hard lattice problem and we can distinguish the lattice-trapdoor from the random lattice i.e by using a known shortest basis for this purpose we can use another method that is known as a gadget based trapdoor for q-ary lattice. For gadget based trapdoor let's study what is gadget matrix. For a modulus q and a base B let l :=[logB(q)]. the gadget vector g belongs to Rl is defined as g := (1,2,4, …2l-1) The gadget matrix dimension is defined as So let us suppose that a matrix A x Rnxn(l+2) that is indistinguishable from a uniform, and a trapdoor B for lattice L(1/q) (A). For any t belongs to Rnq and one can then sample NTRU Trapdoors A simple construction of trapdoor is through NTRU assumption. Let us consider a matrix A = [ 1 h] where Commitments: A commitment scheme is a tuple for the ppt algorithm that depends on three factors For completeness opening any well-formed commitment/ open should recover the message m with the probability time, i.e for any with the overwhelming probability of the random coin ComCK . In order for our system to be efficient, a commitment needs to be binding, that is it should be open to at most 1 message and be able to hide the message that can not be distinguished. Both the binding and hiding can be computational and statistical but our purpose is to focus on the computational aspect. Let us define what are computational binding and computational hiding Computational Hiding: It is hard for any PPT adversary A to generate messages m0 is not equal to m1 such that A can distinguish Com(m0) and Com(m1). Therefore computational hiding can be written as : Computational Binding: it is hard for any adversary A to generate a tuple (c,d,d’) such that Open(c,d)= m , Open(c,d’) = m’ and m m’ hence the computational hiding can be written as In lattice-based commitment we will consider with message space of Rlq We will consider the algorithm that does not include c' However, defining Open statements in this manner will help us out when we discuss the Zero Knowledge based on Lattice Cryptography. Were the prover will only extract c't with small polynomials c'. In practice the C' will be the set of differences of challenges of our proofs which will always have the elements that are small and invertible. Which will be presented as t:= Com(m;r) to denote the commitment of m with the randomness r. A public key encryption scheme is based on three main characteristics of probabilistic polynomial time algorithms. For completeness decrypting any ciphertext should recover the original message m with a strong probability ratio i.e for any (pk, sk) PKESetup (1lambda) and any message m Dec(sk, Enc(pk,m)) = m with a strong probability over the random encryption. A sample algorithm is given below. lattice-based PKE was introduced by Lybashevsky with a ring variant of public-key encryption which used the LWE encryption scheme. Were we present a sample of algorithm of module lattice Correctness: Decryption will only be correct if v-STu = v-STu mod q In that case we have. v-STu = p(ETr+e2-STe1 )+m Let By union bound Since, e,<- DnR,sigma we have The same argument is being applied to ||sT e1 || Since m belongs to Znp and e2 <- DR,sigmak Indistinguishability under chosen-plaintext attack (IND-CPA) Security: For any PPT adversary, A there exist a PPT adversary B for M-LWEq,n,sigma such that: So let us suppose A is an adversary of IND-CPA security of our scheme. We run game in succession Game0: In this case, we use the sample b <- ${0,1} in order to run the experiment Expind-cpa-b(A,lambda). Game1,0<i<k: This game is same as the previous game except for the reason iTh is the column of B is assumed to be taken uniformly in Rnq . recall that bi:= Asi+ei in the previous game. The advantage of A of distinguishing in this game is: Game2: In this game, we take u and v as uniform random vectors. Since Was M-LWEq,n,sigma sample. The advantage of distinguishing this game from previous one is thus Since we know that v is uniform in RKq in Game2 a has no advantage in guessing b AdvAG2 = 0 And after the summation of all inequalities, we get our desired result lattice-based cryptography will help us to build a more secure network in order to protect our data from the quantum computer attack in the near future. In our next research we will be discussing how we can implement lattice-based cryptography in Zero Knowledge and Zero Knowledge proof of knowledge. You can also read upon our latest publication on Kate CommitmentsIntroduction:
Lattices:
B = the basis of lattice L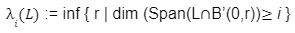 
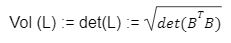
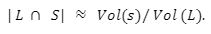
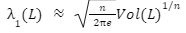
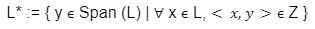
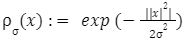
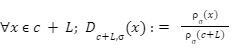
Hard Problem on Lattices:
Cryptographic Problems:
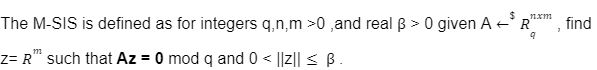
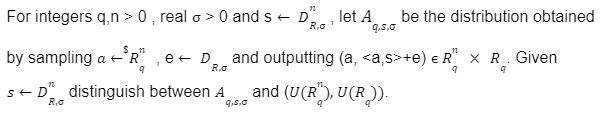
Cryptanalysis:
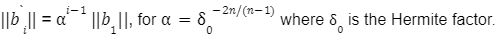
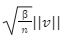
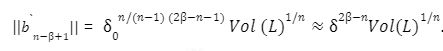
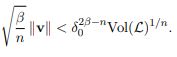
To solve M-SIS we first need to find a vector z belongs to Rm with a norm of B such that Az= 0 mod q which shows that we want to find the shortest lattice L(A)1/q , i.e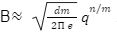 
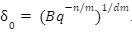
To solve MLWE we notice that A belongs to Rmxn and a sample b:= As + e with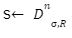
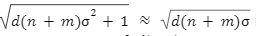
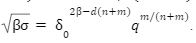
Trapdoors:
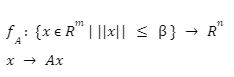
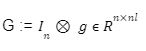
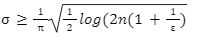
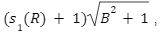
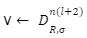such that Av = t mod q by using sample (B,sigma,c) for any 
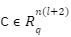such that Ac= t mod q. 
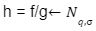if we choose standard deviation of 1.17
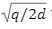then we can easily compute the basis of the lattice L(1/q)A such that 
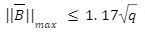while the range of standard deviation is not sufficient to find the basis of the lattice. However, there are no distinguishing attacks that exploit the NTRU structure.Basic Cryptographic Primitives:
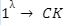helps to generate public key
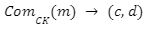generates the commitment c for the message m under the key CK, and an opening d to this commitment.
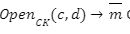opens the commitment c using the opening d. If the commitment is not valid then 
and any message 
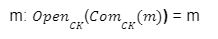
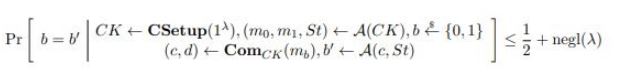
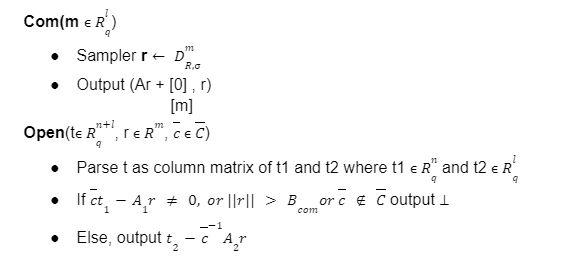
Public Key Encryption:
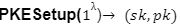generates the public key and secret key
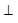if decryption fails.
And v-STu =m mod p. Decryption thus be correct if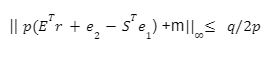
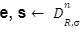be the first column E and S, by applying a union bound it is apparent that proving 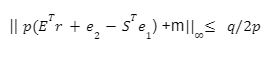with overwhelming probability is sufficient. Let 
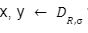we have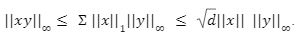 
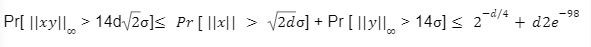
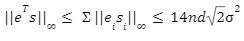
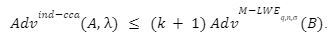
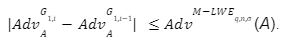
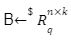in the above game we had 
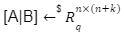and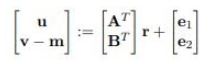 
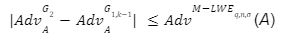
Conclusion:
References:
We develop cutting-edge products for the Web3 ecosystem supported by our extensive research on blockchain core and infrastructure.
