Our previous article was a depiction of how polynomial commitments can create a disruptive path in building stateless clients in ETH 2.0. However, no design is at liberty to flaws. Vitalik in his article has discussed the ideal vector commitment problem[1] which will serve as the context of this article. The kate commitment is a scheme that allows the prover to create a commitment to an evaluation of a polynomial. It is a commitment that has some pre-computed curve points on an elliptic curve[2] at a secret value s, known as the Secret Reference String(SRS). The SRS is a list of successive powers of an unknown quantity s, at some generator points. Here we are taking two bilinear curves with generators g and h producing the SRS. Where, Why are we taking two bilinear curves? Once again, to know this you can refer to our previous article. The t-Strong Log Assumption states that even if the whole world knows these by simply exponentiating those terms by f(x). Polynomial equations can define polynomial functions as: With Reference String the prover can prove In the first step towards Kate commitment the prover can select the polynomial they want to commit and evaluate f at a secret value s, which the prover doesn’t know and has no right to know. For example we have a polynomial : We can simply use the equation given to commit to the polynomial at a secret value s as we know the ith power. So the function f takes an unknown value s and convert it to an elliptic curve point Now a verifier can ask whats the evaluation of z ? so the prover will respond with the answer y and a proof. In this step we have to prove that the value C mentioned above is the true representation of a polynomial in s(the secret setup value). Now after committing a polynomial the verifier will ask the prover to verify the commitment C was an actual evaluation of some polynomial at some other value z.To prove, the prover can perform a quick calculation which could only work only if C is truly equals to Because z is a root of f(x)-f(z), then the prover will create a quotient polynomial: But one question to ask here is that how could the above equation verify the soundness and validity of the proof? Well it is proving. For a polynomial f(x) if a prover calculate the evaluation at the point z then F(x) - F(z) must be divisible by x-z, Because it is obvious. Now, the verifier will be provided with the following information by the prover. By the above information the verifier can easily verify the validity of a commitment. It is because if the f(z) is not the claimed evaluation then the For a verifier to check the authentication of proof he must needs to check the relation between original commitment C and the quotient The verifier can not compute their Q(s) because they can not divide the commitment by s-z as they dont know s. But thanks to pairings we can use multiplication instead of division by holding the below relation. And with pairing e([f(s)]-[f(z)],[1])=e([π],[(s-z)]) Kate Commitment is no doubt an efficient polynomial scheme for stateless clients. However, using it alone still doesn’t solve the huge witness size problem. With respect to this, the Ethereum community has introduced a structure called “Verkle Tree” which makes efficient use of this polynomial scheme. We are leaving this debate for our next post.Kate Commitments
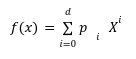
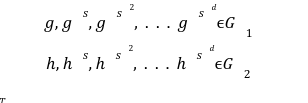
![]()
The t-Strong Discrete Log Assumption
![]() elliptic curve points , no one can ever be able to trace back out s. This reference string provides us the little monomial terms[3] in the form of gsifrom the generator point i=0 to the i=d where, d is the highest degree of polynomial we want to reach. These monomial terms
elliptic curve points , no one can ever be able to trace back out s. This reference string provides us the little monomial terms[3] in the form of gsifrom the generator point i=0 to the i=d where, d is the highest degree of polynomial we want to reach. These monomial terms ![]() can also used to create the encrypted evaluations of a given polynomial
can also used to create the encrypted evaluations of a given polynomial 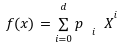
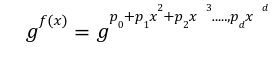
![]() till the degree of function f(x) <d. Now let’s structure the way a prover can commit to the polynomial and generate opening proof while the verifier can verify the opening at any point of state.
till the degree of function f(x) <d. Now let’s structure the way a prover can commit to the polynomial and generate opening proof while the verifier can verify the opening at any point of state. Step1 Commit f
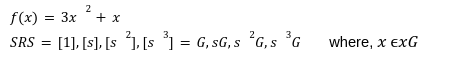
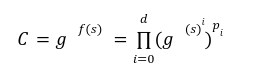
![]()
Step2 To Prove f(z)=y
The Proof
![]()
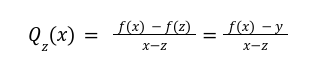
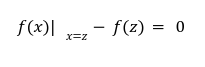
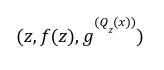
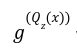 will give a negative monomial power, keeping in mind there were no negative powers in the reference string.
will give a negative monomial power, keeping in mind there were no negative powers in the reference string.Up Till Now:
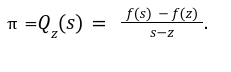
Step3 To Verify
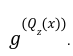 But how? well what we are trying to do is to check whether the prover has completely divided the term
But how? well what we are trying to do is to check whether the prover has completely divided the term ![]() with remainder =0.
with remainder =0. Note:
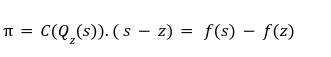
Conclusion
References


