ZK-SNARKs are mostly popular for publicly verifiable computations. They rely on common reference strings (CRS) for proving and verifying. Subversion in these parameters leads to forged proofs and potentially billions of dollars in theft. In our previous article, we have discussed how a trusted setup works and how we generate a CSR mathematically. Although there are constructions that allow transparent parameter generation such as STARKs and Bulletproofs, however, these constructions have little to nothing practical efficiency. Early constructions such as Groth16 are a fixed NP-relation problem. In other words, these proofs are specific to a given program. Changing a program means discarding the old parameters and generating new ones. Thus the flexibility of these constructions is very limited. This article is a short and gentle introduction of the difference between MPC[BGM17] vs MMORP and why MMORPG is also termed as Power of Tau. Till now the most used protocol for generating this CRS is Multi-party computation. It is a scheme which requires a one-time setup for each statement. MPC is a typical interactive protocol which involves multiple parties who contribute randomness to iteratively construct the CRS. These protocols guarantee soundness i.e. that proofs cannot be forged when at least one participant is honest, and guarantee zero-knowledge-ness even if none of the participants are honest. However, these protocols fundamentally cannot scale beyond a handful of participants and can be too expensive to perform for just one or two participants. In MPC there are few restrictions on participants. For instance, to restrict the attackers the participants of the scheme must commit to their share of the parameters in advance and maintain availability and security throughout the duration of the protocol even after the majority of their individual computation has already been completed. In this scheme even if a single participant aborts, the entire protocol must restart. So the main issues are: Here, you can visualize the working of the original BGM17 protocol. Note: MMORPG was first introduced for Zcash ceremony sapling where a central “coordinator” manages messages between the participants. The CRS is generated in two phases. The first phase, referred to as “Powers of Tau”, produces generic setup parameters that can be used for all circuits of the scheme, up to a given size. The second phase converts the output of the Powers of Tau phase into an NP-relation-specific CRS. For universal SNARKs we do not need to go for the second phase of the setup. In 2017 Sean Bowe, Ariel Gabrizon and Ian Miers introduced a second family of MPC protocols called MMORPG specifically designed for pairing based universal ZK-SNARKs which is often termed as “Power of Tau”. In power of Tau contributors do not need to be selected in advance, instead the protocol uses a random beacon that produces public, random values at set intervals to enable a continuous ceremony. Participants, therefore, do not always need to be available and online. It is a more scalable multi-party computation (MPC) protocol, secure in the random beacon model, which omits the precommitment phase. The protocol proves that security holds even if an adversary has some influence on the beacon. The power of Tau offers a serialized process for CRS. To get the idea, consider an example. We have a CRS that only consists of the elements s.g1 and αP(s).g1where g1 is the generator of group G1 with order p and are the uniform elements of field F*P. The polynomial we have is P(x):=3x+5 over FP. The main protocol with three honest participants will look like this: The CRS in this example is a double (s.g1,αP(s).g1) where s can be s=sN+1, sN, sN-1, , , s1 and α=αN+1, αN, αN-1, , , α1 are scalar multiples that can be cumulatively compound in a serial manner. The protocol consists of 2 round-robin phases. In phase one, each participant communicates with the other to compute s · g1. In between phase 1 and 2, the untrusted coordinator computes P(s) · g1. Finally, in phase 2, a set of participants compute αP(s) · g1. In each phase, participants send one message and receive one message. So there is a central coordinator which invokes the random beacon after every set interval to add the randomness which excludes the attacks of any malicious party in the ceremony. For the detailed working of MPC protocol you can refer to this research paper. Innovations in setup ceremonies are getting efficient with a breathtaking pace. Schemes are getting more efficient, making future development of SNARKs more practical. Multi-Party Computation
Issues with MPC [BGM17]
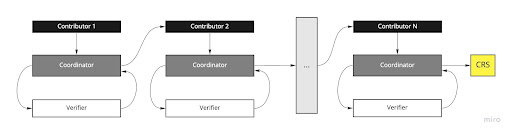
A New Scalable MPC Protocol [MMORPG]
What is MMORPG
Example:
The Working of Protocol for Omitting Pre-commitment Phase

References


