Special thanks to Shakeib Shaida and Zainab Hasan for reviewing my article. Zero-knowledge proofs are cryptographically advanced proofs which are being used by many blockchain protocols to attain privacy and scalability. Though the more these proofs look sophisticated, the more complexity is inherent within them. In the second series of our publication, we are going to discuss the pre-processing of ZK-SNARK and how a multi-trusted computation setup really works. Previously, in our series of ZK- SNARK articles I have explained how a basic ZK protocol works and we have also discussed some scenarios where a prover can cheat and forge the proofs. However, we have not discussed the origination point of the proving polynomial P(x) and why it is important. To begin with, we know that zero-knowledge proofs mainly depend on three algorithms. In this article, I will discuss the importance of keys and why trusted setup is a better trade-off for security. We will also see the initial mathematical structure of Multi-trusted party computation. Before discussing the key generation process in ZK-SNARK using MPC we need to understand that there are multiple methods of generating keys in a way which maximize the security and efficiency of the system but I will argue that the pre-processing of ZK-SNARK using MPC reduces the chances of failure modes because of two reasons. However, whether you opt for trustless or trusted setup, you must consider the security and efficiency of the scheme to be the top priority. In blockchain, we mostly deal with non-interactive zero-knowledge proofs(NIZK). There are multiple applications that are using these NIZKs(you can read about them from zkp.science). These proofs are generated once and can be verified by any verifier at any point in time. This requires the prover and verifier to have some common knowledge. This common knowledge is also known as common reference string(CRS) which indicates that the keys generated for both prover and verifier are for the same setup. So now let's discuss why we need a trusted setup? It is an aspect of soundness that the prover might cheat the verifier with fake proof if the verifier doesn’t know exactly which statement is being proven. One way is to give the full representation of the statement to the verifier, which is not feasible if we want to make a verifier a stateless node( in terms of ETH2). This will also result in slow verification and low latency. There are three possible ways to ensure that the verifier knows what is being proven. The verifier gets a full representation of the relation, which makes the verifier running time linear to the relation size. One example of the above statement is “bulletproofs”. Bulletproofs, also called “range proofs”, are best suited for small statements. Bulletproofs produce a URS(uniform random string), which is a kind of CRS which does not encode the relation and hence doesn’t provide succinctness. To read about URS see this. The verifier gets a succinct and basic representation of a computation which is being repeated many times. For example, proving the computation of 100 commitments will require only one commitment as the relation which is expressed succinctly. Proof systems based on Probabilistically Checkable Proofs, for which the statement can be represented in an algebraic form lies in this category ([BCGTV12] and FRI-based STARK), which then further generates a URS with pre-processing that is sublinear on the size of the relation. SNARKs can achieve the succitness for any relation if the statement is not short or even if the statement is not repetitive. To achieve this, the verifier is provided with a summary of the relation, meaning that the pre-processing digests all the relation into some short random string. The pre-processing generates SRS i.e. secret random string, that is linear in the relation to the prover while the verifier running time is short. The main point is if one wants to have a short verifier running time with a relation which is not uniform then, one can not get rid of the pre-processing of the SNARKs. The problem lies with the balance of privacy and trust. The prover is liable to not forge the proof while preserving the knowledge. Generally, zero-knowledge proofs use some randomness to challenge the prover. In case of pre-processing the randomness is to be generated in advance and this can be verified publicly. On the other hand in URS, the randomness is given at the time of proving. The SRS trusted setup depends on some non-public randomness to avoid the backdoor of generating fake proofs. One can argue that pre-processing kills the purpose of zero-knowledge proofs in a public system where anybody can be the prover or verifier. Well this is true and to accommodate this, SNARKs that have secret reference strings are best coupled with multi-party computation(MPC). Multi-party computation is a ceremony where large numbers of parties come together to minimize the trust assumptions and ensure that even if only one person behaves honestly(destroying his local secret) the system will remain secure. Now lets understand how a trusted setup works mathematically. Let us assume that we have a trusted party which selects the secret s and α. What are these secret s and α please refer to our previous article on how a typical SNARK works. As soon as the α and s powers of all inputs are encrypted These parameters are what we call SRS. The CRS is divided into two groups: Having the verification key the verifier can easily process the received encrypted polynomials evaluation gp,gh,gp` from the prover. Again for better understanding of the continuity of the protocol please refer to my previous article. Now the protocol will look like this: Although the trusted setup is efficient, it is not effective to ensure whether the single party that has computed this CRS has deleted α and s. Currently there is no way to prove that. Hence it is necessary to restrict the dishonest party from making false proofs. MPC allows us to generate composite CRS by using mathematical tools to restrict the parties. Let's get this with an example. Consider Alice, Bob and Carol with corresponding indices A, B and C. As the result of the above protocol, we have si=siAsiBsiC andα=αAαBαC and no one can extract the secret parameters of others. So in order to learn about the s and α one has to collude with all the other participants. So even if one participant is honest the protocol will remain secure. The main issue with this approach is how can we make sure that the participants remain consistent with every value of CRS, because an adversary can sample multiple different s1s2s3, . . and α1α2α3, . . . and use them randomly for different powers of s, making CRS invalid. Luckily, since we can multiply encrypted values using pairings we can perform the consistency check, starting with the first parameter and ensuring that the very next is derived with the last one. Let's see how we can achieve this mathematically. Although here we have restricted each party to be consistent with their CRS, however, we still haven’t enforced that use of previous CRS for publishing the next one. Hence, any adversary in the middle or end can produce a CRS from scratch and pretend to be the first contributor in the chain. Therefore, being the only one to know the s and α parameters of the setup. We can address this issue by restricting the participants to publish their encrypted parameters except for the first parameter. For example, in the above example except Alice, Bob and Carol, all publish their encrypted parameters. With this they will also publish the augmented output which in the above example is: This will validate that Bob's CRS is the augmented version of Alice’s CRS. This is a powerful scheme which remains secure as long as one party remains honest and does not depend on any single party. This qualifies any party to be part of this setup and ensure that nobody is sabotaging the final CRS. So shall we look at how our final protocol design for a SNARK will look like? Before proceeding you must look into this article which is the prerequisite to the further working of this article. After forming our polynomial P(x) and agreeing upon the target polynomial t(x), we now move towards the concrete steps below. We have successfully constructed a succinct non-interactive zero-knowledge protocol for a polynomial based problem. The verifier can be convinced that the prover has a valid polynomial without knowing anything about it. This provides us a universal scheme for multiple SNARK implementations. 2. Diving into the snarks setup phase 4. EPrint IACR
The Need for a Trusted Setup
Full Statement
Succinct Statement
Pre-Processing
Why Pre-processing?
What is MPC?
Trusted Party Setup without MPC
![]() the raw values must be deleted.
the raw values must be deleted.
![]()
![]()
Trusted Setup With MPC
![]()
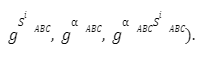
Problem 1
Solution
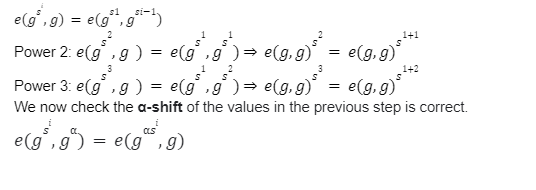
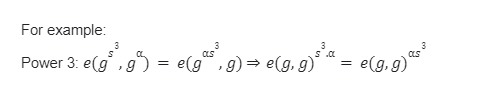
Problem 2
Solution
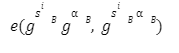
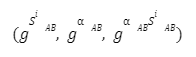
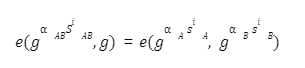
SNARK (Succinct Non-Interactive Argument of Knowledge)
Setup Process
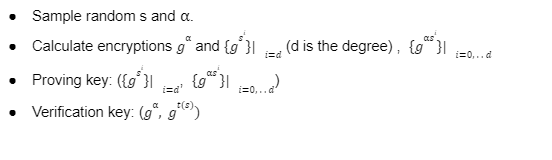
Proving Process

Verification Process

Conclusion
References


