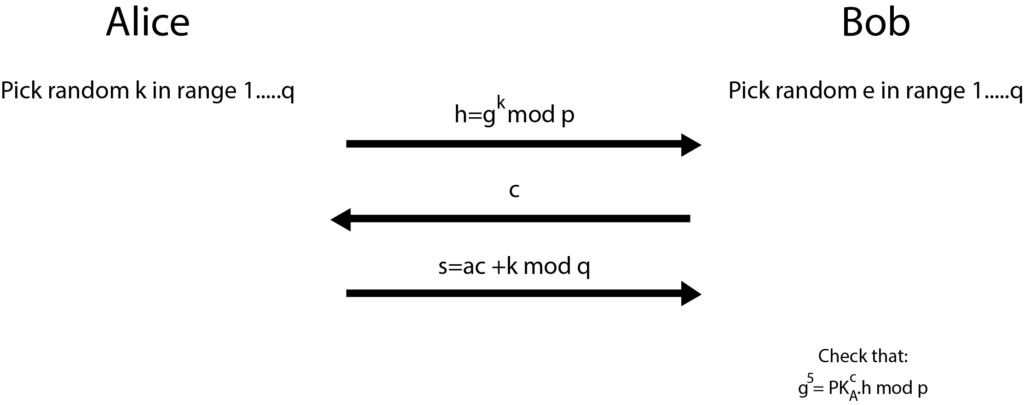
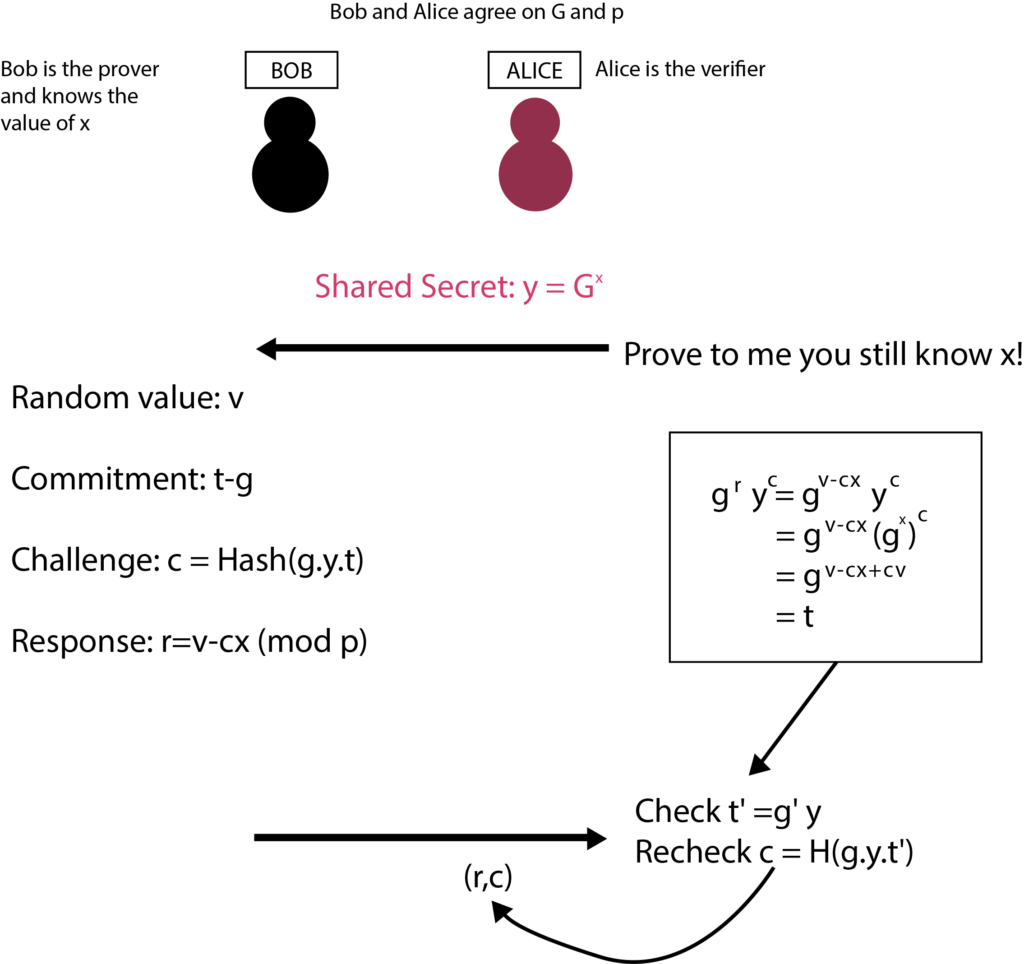
Learning zero knowledge can feel like an impossible task, especially for people who have very little exposure to cryptography or in academia. And the resources are somewhat scattered as well. The main hurdle is understanding the concept and proving relevance to oneself about the usage. This article will assist in painting a mental picture of the Zero-Knowledge journey that’ll go through the concept of privacy while explaining how it is implemented and what the mindset is while thinking of zero-knowledge-proof systems, and how one can start the development journey as well. Privacy means a state in which you are not observed or disturbed by others. We won’t be discussing the definition of privacy, whereas we’ll be talking about how privacy is perceived in a blockchain? And what do we mean when we say our data should be private? Blockchain provides anonymity out of the box in the form of a public key associated with your wallet. But this anonymity can be observed by others as the data and state of blockchain is public (in all public blockchains). And if you transfer your funds from a centralized exchange to your EOA, then an association will be made. Companies such as Chainalysis offer such services in the market as well. Privacy in blockchain can be achieved in three different areas Consider an ideal blockchain in which you are sending a transaction; the address of the sender, receiver, the amount, and the blockchain state is hidden. Then one can ask how the data validation and consensus will be reached? If we think from a realistic perspective, we might also have to consider the constraints of consensus, scalability, data availability, and computation overhead. So to define the scope of privacy, we must try to answer the following questions. The following image shows how privacy in the different blockchains is implemented and at what stage as well. If we talk about it in general terms, the proof is like a witness which we have when we want to prove any statement. Even in the real world as well. There are two kinds of statements that can be proven. Facts and knowledge. Statements such as, “I know a number N which is in the set of composite numbers”. These kinds of statements can be translated into SAT. Statements such as, “I know the factorization of N”. These kinds of statements are based upon the knowledge of the prover. Statements like these have a broader scope. The actor in the system has a witness about a specific problem that they want to prove. Prover in various cases is referred to as a Simulator. A simulator is a hypothetical machine that is designed in such a way that it behaves the same even when there’s no verifier as well. Simulators have special powers as compared to normal provers. They can’t predict the challenge, but they can hypothetically rewind the time back and generate the same proof again. The actor in the system with which the prover will be interacting. Knowledge extractor is also a kind of verifier that is used in special cases to extract knowledge from the prover. If a knowledge extractor learns anything beyond the fact that statement is true or not, then the proof system is not designed correctly from the perspective of zero-knowledge. Completeness: If x ∈ L, then ∃x’, V(x’,π) = ACCEPT For every x in language L, the proof will be accepted. If the prover is dishonest and tries to prove x out of the language then it will get rejected. Soundness: If x ∉ L, then ∀x’, V(x’,π) = REJECT Verifier will only be convinced if the statement is true, and doesn’t accept values out of the language. Knowledge extractor enters the scene when it comes to proving the soundness of the algorithm. The role of knowledge extractor doesn’t have to be present at all times as well. Here π is the proof or the witness. But for a proof system to become zero-knowledge, it must also exhibit one more property: zero-knowledge. No other knowledge is revealed while proving other than the fact that the statement is true or not. In the 1988 paper by Goldwasser, Micali, and Rackoff [GMR], they introduced the concept of an interactive proof system. This proof system enabled the prover-enabled prover to convince the verifier about the validity of the problem statement through witnesses and a finite number of interactions. Diffie-Hellman provided the world of cryptography a framework for the message passing between two parties of the network in a mathematically mathematical secure manner. And it proved to be a very mere base for the future algorithms and design architecture of different concepts as well. such as asymmetric key cryptography, and signature verification. If we talk about signature verification; specifically the identification of information we have different algorithms as well. Ssuch as DSA, ECDSA, etc. But these verification methods are based on the Schnorr identification protocol. Alice wants to prove the ownership of her private keys to Bob. Let’s take a look at an example and see what makes the Schnorr identification protocol an interactive zero-knowledge setup. Alice picks up g (generator number), a (random number), and p and q (prime number of the field Z). She published g, p and q computes PKA=ga mod P, SKA=a Whereas; PKA is the public key, and SKA is the secret key. Now she wants to prove the ownership of the key to the verifier. gs ≡ PK cA . h mod p gs ≡ PK cA . h mod p gac+k ≡ (ga)c. gk mod p gac+k ≡ gac+k mod p As we can see, Bob just needs the public key of Alice, challenge c, which he gave to Alice and computed h to verify. Let’s break down the protocol and see how it stands against the three pillars of zero-knowledge-based proof systems. The machine of the prover is designed in a way that it can perform these tasks: This is how the simulator is designed. The knowledge extractor’s core purpose is to extract the knowledge out of the system. But we need to understand what kind of knowledge the knowledge extractor can learn? If the verifier sends c, and the simulator computes the s with the same k. The verifier can learn about the secret key a. This is something the simulator has to tackle on its end. It has to make sure to compute the different k at the start of each round. One can argue why will the verifier go onto another round after the completion of the first? The answer is simple. Verifier is not convinced yet. This brings us to the very important point of interactive proofs, and that is, the convincing is based on probabilistic results. Interactive protocols require verifier and prover to be online at the same time. But what if there’s no verifier online and the prover wants any verifier to prove. In the 1980s, Fiat Shamir noted that the inclusion of a hash function would not require interaction between parties. Thus if we introduce the concept of the Random Oracle Model (ROM) in the verifier and prover, we can eliminate the need for interaction. In non-interactive proof systems, ROM is not used; rather CRS (Common Reference String) is used to set up the trusted proof system. We won’t be diving deep into the working of a random oracle, but for the sake of the mental picture, it is a common registry of function f(x) with deterministic result y in the field F. Both verifier and prover have access to this machine. How does this concept of randomness eliminate the need for interaction? In the above picture, FIAT Shamir is explained using the random oracle model. The challenge c is being generated using a hash function. Now the prover doesn’t require a challenge c from the verifier to compute upon. The other working of the protocol remains the same. For any decision problem of which the proof can be verified in polynomial time can be converted to zkp (zero-knowledge proof). The fact that proofs need to be verified in a polynomial time, but the behavior of the system is non-deterministic, so for the construction of zkp, NP-Complete problems are chosen. The statements are converted into NP-Complete problems, then into boolean circuits. This graph coloring problem is an example of interactive proofs. If you want to see how graph coloring works, you can check it here. Let’s break down the graph coloring problem from the perspective of the prover and verifier. If you want to try out the sudoku puzzle you can check it out here. Repository for this above example can be found here. This sudoku example is how the ZK-SNARK system works in a holistic view. ZK-SNARK stands for Zero-Knowledge Succinct Non-interactive ARgument of Knowledge. If you are studying ZK after some theoretical research, you’ll be stumbling upon this topic. So let’s discuss what ZK-SNARK is and how to perceive the practical ecosystem. As we have discussed above, there are two kinds of proof systems. Interactive and non-interactive. In order to understand the algorithms clearly, we categorize them from two perspectives. Class of Construct and Construct Mechanism. There are two “classes of the construct.” Interactive and non-interactive. The Non-interactive class of construct is ZK-SNARK. ZK-SNARK is not itself anything. It is an umbrella of algorithms. I would recommend that you not think of the ecosystem in terms of classifications. Classifications are helpful for examples and theoretical explanations. But once the practical implementations and research come, there are many other criteria and building blocks present on which the system is judged. For example: You can learn more about different implementations of zkps here. ZK-STARK stands for Zero-Knowledge Succinct Transparent ARgument of Knowledge. ZK-STARK is not a categorization, it is a “construct mechanism” which is based on the interactiveness of the protocol through Interactive Oracle Proofs (IOPs). You can read more about ZK-STARKs here. ZCash is one of the biggest mainstream examples of the usage of ZK-SNARKS to provide privacy to the user, it uses Groth16 to provide shielded transactions to the user. In the shielded transactions in which addresses of participants and amounts are hidden from the network. If you recall the concept of privacy discussed earlier in this article. ZCash is providing privacy in hiding the identity, tx data, and blockchain state. Only the UTXO’s commitment hashes are stored in the blockchain as: Commitment = Hash(spender’s address, nonce, rho), rho is a secret number that will allow the spender to create a nullifier against this UTXO. Creating a nullifier basically means that you are giving proof that you have the authority to spend this UTXO. You can read in detail how the data is stored and the working of transactions here. There are very different aspects of research and application development in the SNARK world. If you are targeting application development using ZK-SNARKS. It has some base steps which are needed to be followed in order to implement the application. We won’t be discussing each and every step, but we need to have a clear understanding of the need for every step. Computation is the mathematical problem that you want to prove a solution for in the system. As you might remember, we discussed earlier as well that after the conversion of problems into mathematical statements, boolean circuits are being made. On the very low level, the snark circuit only supports four operands and three variable handling per line of execution. Y = X (OP) Z; OP = + - / * After the flattening of your equation, constraints will be applied in order to check if the values are flowing correctly or not in the system. For that, R1CS is used. Discussion of R1CS and the constructions of QAP for commitments are out of scope for this article. You can read more about the flattening process here. You can read more about the constructions of QAP here. And you can understand the calculation of R1CS here. After generating the commitments, you need a proof system, and for SNARKs, Linear PCPs are used. Different implementations of SNARKs use different proof systems. Having the knowledge about the components and the usage is necessary to architect the solution, which is then complemented by a wide range of libraries and languages for writing circuits. Different implementations of proving systems and libraries for writing circuits can be studied from zkp.science. Step by step R1CS tutorial by arkworks Thinking about zero-knowledge as a perspective rather than a concept facilitates segmenting different algorithms and can help us to brainstorm on different problems from the perspective of 3 pillars. Zero-knowledge itself is not a problem. Different construct mechanisms are. And different construct mechanisms follow different design patterns. Construct mechanisms have a lot of open areas for R&D. I would like to acknowledge Zainab Hasan, Rabia Fatima for proofreading the article. And Filza Manzoor for working alongside me in the understanding of different cryptographic algorithms. Introduction
Perception of Privacy
Zero Knowledge; Nitpicking the Details
Proof
Proof of Fact
Proof of Knowledge
Prover
Verifier
Properties of Zero Knowledge
Interactive Zero Knowledge
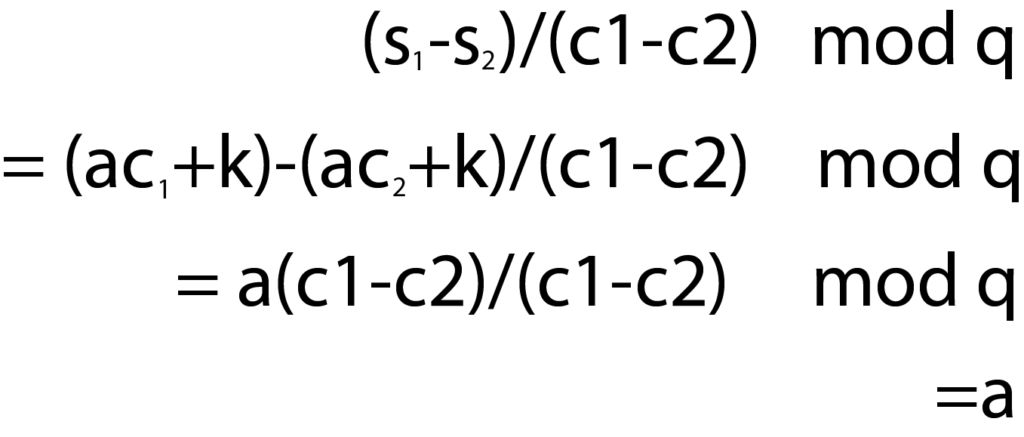
Non-interactive Zero Knowledge
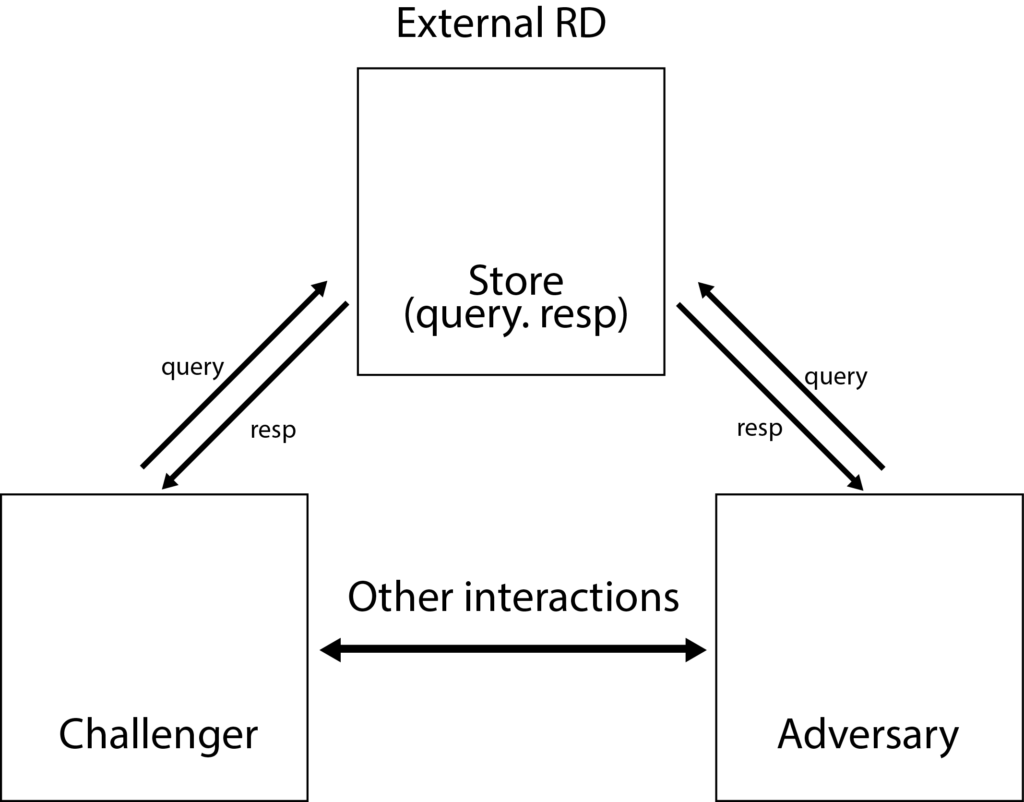
Understanding with Example
Graph Coloring Problem
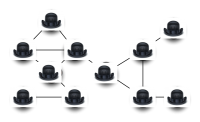
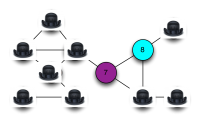
Sudoku Problem
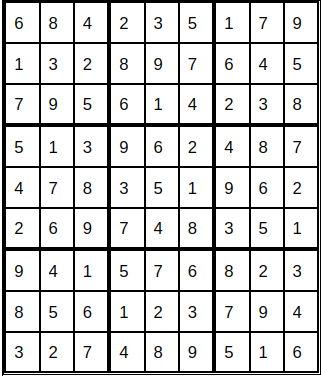
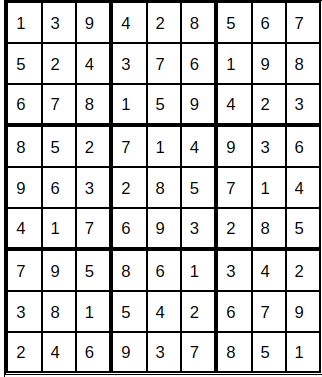
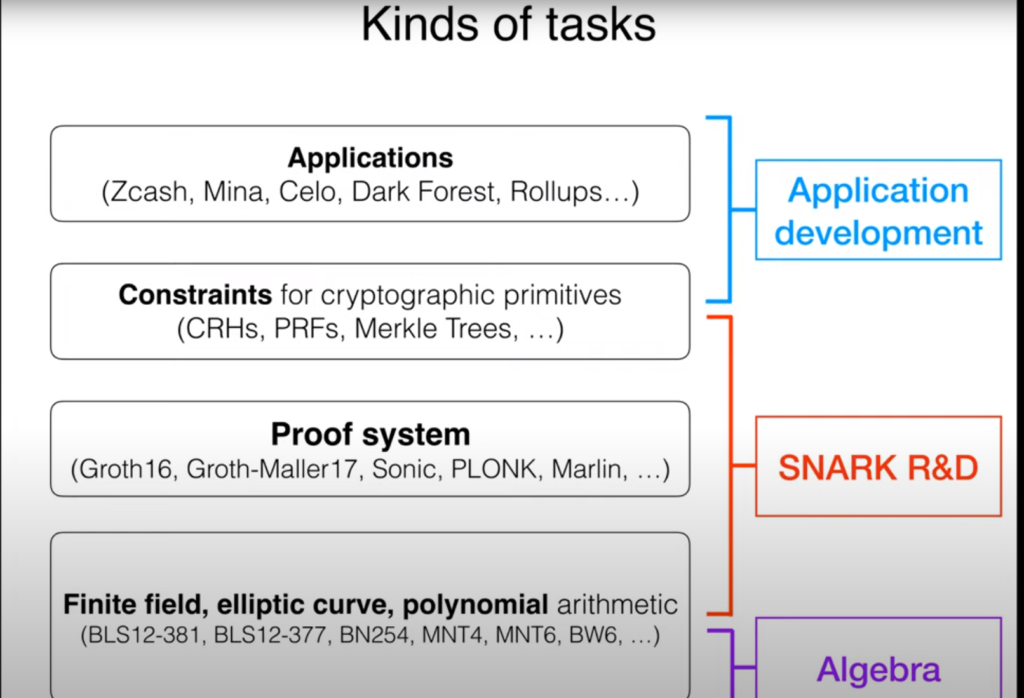
Perceiving the Ecosystem
ZCash
Development Head Start
Conclusion


